Identity
of Generated Objects – Gain and Loss Along Transformational Chains.
Prof. Dr. H.
Dehlinger
Department of Product
Design, Kunsthochschule Kassel, Kassel, Deutschland.
e-mail dehling@uni-kassel.de
Dipl. Des. O. Werner
Department of
Product Design, Kunsthochschule Kassel, Kassel, Deutschland.
e-mail ole_werner@web.de.
Abstract
Simple transformations applied to a structure
may have dramatic effects on the visual appearance and other properties of the
structure. They may result in an increase or in a loss of properties
contributing to the “identity” of the structure. Starting from some objects
(generated and adopted), such gain and loss of identity along transformational
chains is experimentally discussed and demonstrated. Many questions are raised
and some hypothetical conjectures are attempted. This is work in progress.
1. Part One: construction and
reconstruction of identity
To prove our identity, we possess an
ID card, a passport or some other sort of document, usually with a picture,
with information about height, the colour of the eyes and other information of
personal characteristics. The „proof of identity“ is presenting such a document
issued by an authority. Sometimes a fingerprint, voice samples or an analysis
of the genetic code is used. If identity is to be ascertained, coordinates of
identity (I1, I2,
I3, ... In) are compared and checked against the
pretended identity. They are listed and are compared, until a certain threshold
of doubt is eliminated and we are persuaded that the presented coordinates
proof the pretended identity. Identity is uniqueness. The Greek root, eidos,
idea, also signifies form. If all things possess identity, then the relevant
knowledge from which we draw the comparative coordinates belong to a very large
domain, and this knowledge is structured on the ground of historical / cultural
reasons in a certain manner. One can postulate that the modus procedendi of
constructing / reconstructing an identity will depend on the logics one chooses
to follow. The analysis of the trains of thought which lead to the construction
/ reconstruction of identity as a result, puts the identification of rules of
the nature of this action to the task. Its concern is a common problem to be
found in the work of engineers, planners and all kinds of designers: the
generation of a design.
The construction of identity can be formulated
as an imperative:
(i) Design an object Oj that has an
identity like object Ok.
Such an object Oj is in some way
partially identical with the reference-object Ok. By pointing to a
reference Ok, which may be
analysed subsequently, a list of coordinates of identity may be arrived at. It
remains however open, which ones are chosen by the designer to fulfil the
demand for identity. For most design problems however, at least for all the
ones that „matter“, there is no reference object whatsoever.
Partial identity may be measured on an ordinal
scale e.g. from weak to strong, and arbitrary weak partial identities may be
constructed.
Instead of relying on an arbitrary set of
identity coordinates, we may demand that a limited, but specified subset of
characteristics is fulfilled exactly:
(ii) Design an object Ok, that has
exactly the identity coordinates (I1, I2, I3,
... In).
Or, in a weaker form:
(iia) Design an object Ok with has
identity coordinates similar to (I1, I2, I3,
... In).
The search for relative identity is not easy to
grasp. It can lead via associations / terms of reference to conceptional units,
which are located far away from the starting point, and it can lead into remote
corners of the search space. It is not unrealistic to assume that very
innovative ideas have a very large conceptional distance from the established
knowledge structure of a field. An innovative designer then has to produce
"conceptional chains" (associative transformations) over large
classificational distances, which (possibly) become the more fruitful; the more
daring they ignore the established borders.
A more exact
view of the term “identity” and of the scales on which it can be
measured and compared, leads to different possibilities of logical distinctions
with regard to degrees of identity. They are to be outlined in the following
considerations.
(a) In the sense of a binary
decision, and in a not further specified manner, Oi and Oj may be claimed
identical or “of the same identity”
(b) Comparatively one can
say: Oi has more from the
identity of Oj than from Ok .
(c)
This can be differentiated further, if we introduce discrete levels
(absolutely identical, very identical,
a little bit identical ...) or use a scale from 0 to 1 as a measure of
"relative identity". We then can formulate statements (see above)
like: Oi and Oj are “relatively identical”, with reference to
the identity coordinates I1,
I2, I3 ..., In. Oi and Oj share a common set of
coordinates.
Still further types of
identities can be distinguished, e.g:
(d) Structural
identity. Two objects are structurally identical, if they can be decomposed
into structural components with a common mapping.
(e) Complementary identity.
Two objects are complementary identical, if they fulfill their function only
together and in coexistence.
(f) Substitutive identity.
Two objects are substitutive identical, if one can replace the other. If the
possibility of the substitution refers only to partial aspects, one can speak
also of partial substitutive identity.
(g) And others more.
Designers usually and gladly fall back on the
type of unspecified identity, which can only be measured on a binary nominal
scale as "is existing" or "is not existing". In this way
the fog of mystery, surrounding the creative act is maintained, which appears
to be intended. If one tries to find a code for the construction of identity,
the only way seems to be the one to explicit define the coordinates of a
certain and specific identity. In the following parts 2 and 3, some experiments
will be discussed which point into this direction.
1.
Part two:
Transformations and Complexity
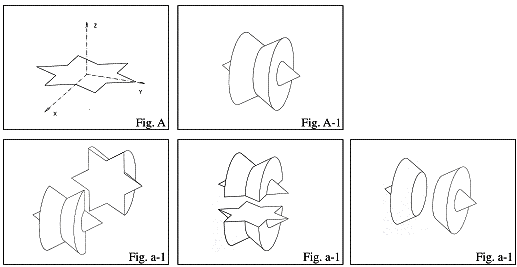
Abb1. Rotation und Teilung
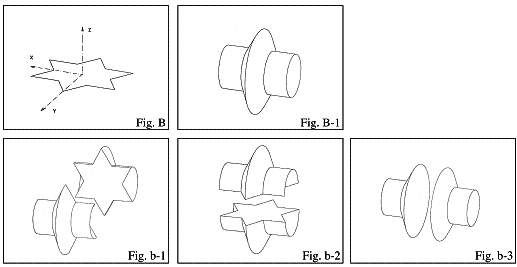
Abb2.
Rotation und Teilung
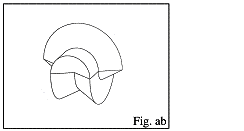
Abb3.
Rekombination
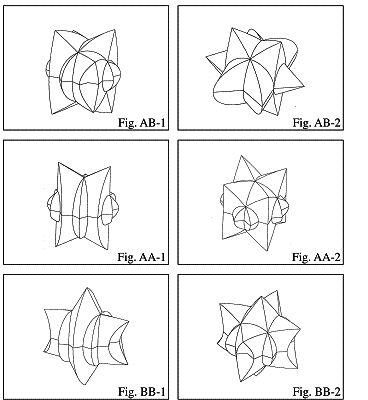
Abb4.:
Schnittmengen
The designer is constantly struggling to
arrange himself between the world of concepts and ideas - all which is before
his mental eye only - and the world of explicit public presentation of this
ideas to everyone. There is always the problem to confront him and the others
with a presentable explicit picture of things, which do not exist yet at all at
a given time frame. It requires a fundamental understanding of spatial
relationships and arrangements in abstract terms without direct seizure of an
object. The ability to order three-dimensional things mentally, to present
them, is a condition for performing the act of representation. Only which is
existent as a conception already, is also representable, and presentations are
an indispensable aid in the design process. Understanding of the premises is
linked with our experiences and it is based closely on the availability of
certain arranging and explaining information. Spatial representations with the
aid of the computer presuppose an accurate imagination of the objects to be
constructed.
If a construction is however "entered" into the machine, it can
be changed and supplemented fast, without much effort, and under a great
variety of objectives. This is the big potential of the computer-aided
representation. It is simply and instantly available. The representation
process itself does not have to struggle with the actual construction of the
object as compared to a process, carried out by hand. The structural division
between presentation of a visual image and construction of the visual image in
the machine, allows to generate images of objects without having a clear
picture of the generated image at all. It is conceivable then, to write down or
to plan an abstract sequence of construction-operations (we can call this a
preconceived programme), without having in advance a clear idea about the
outcome. Only on the screen will this idea be formed by the generated
results. Such a preconceived programme,
carefully designed and tested, is a form-generator, which is required in all
generative design approaches. We assume here such a generator to be a highly
interesting instrument to engage in a game of exchange between human
imaginative power and visual calculative representation on the screen.
For the example presented below, we use a
"programmme" which essentially consists of a sequence of geometrical
operations, which can be carried out in short time and directly in front of the
screen. On the basis of a simple two-dimensional figure, we generate increasingly
more complicated three-dimensional objects.
The two questions in which we are interested
are: Is it possible for us, to imagine the identity of the generated objects
solely on the basis of a given rule of transformation? And, vice versa: Is it possible by looking
at the result, to identify the transformational rule responsible for the
result?
[Please
refer to the German version of the paper regarding all figures.]
The experiments [1] show, that our imaginative
power is surprisingly limited, which we will demonstrate with the following
sequences of images.
The basis for all the constructed
figures is the regular and well known “star” with six spikes. It is
constructible with a simple rule from an equal sided triangle: Draw on the
middle third of each side again an equal sided triangle [Abb. 1. Fig. A / Abb. 2. Fig. B]. In a further step, three-dimensional
objects are generated from this figure by rotations on two axes of symmetry
[Abb. 1. Fig. A-1 / Abb. 2. Fig. B-1].
If we cut the
generated object along the planes of the coordinate system, we get two
identical objects each [Abb. 1. Fig.
a-1, Fig. a-2, Fig. a-3 / Abb. 2. Fig. b-1, Fig. b-2, Fig. b-3].
The existence of identical planes after cutting, allow new combinations of either equal or different parts. A multitude of new and surprising objects may be generated. Abb.1 is showing a combination of Fig. a-1 with Fig. b-2.
The forms of Fig. A and Fig. B are now merged into one Volume in 300 resp. 600, and the new object is calculated. The new object is formed from the volumes shared by both of the figures we started off with.
· Fig. AB-1: merged from Fig. A-1 und B-1, angel of rotation 30°
· Fig. AB-2: merged from Fig. A-1 und B-1, angel of rotation 90°
· Fig. AA-1: merged from Fig. A-1 und A-1, angel of rotation 30°
· Fig. AA-2: merged from Fig. A-1 und A-1, angel of rotation 90°
· Fig. BB-1: merged from Fig. B-1 und B-1, angel of rotation 30°
· Fig. BB-2: merged from Fig. B-1 und B-1, angel of rotation 90°
For the generation of those rather complex forms only two operations are necessary (one rotation, one Boole operation each). Keeping this in mind, the destructive power of longer transformational chains on the identity of the object, as well as the fast emergence of new identities for generated objects becomes apparent.
2. Part Three: Transformations and Identity

Abb1.:
Beispiele für gefundene Trockenformen aus der Natur, die in ein Diarähmchen
eingespannt wurden [2]

Abb.2:
Blatt und Blattraum [3]

Abb. 3 „Formen 1“ [4]

Abb. 4 „Formen 2“
[4]

Abb. 5 „Kugel“
[4]

Abb. 6 „Stadt-Raum“ [5]

Abb. 7 „Hochhaus“
[5]

Abb. 8
„Gebäude“ [5]

Abb. 9 „Explosion“[6]
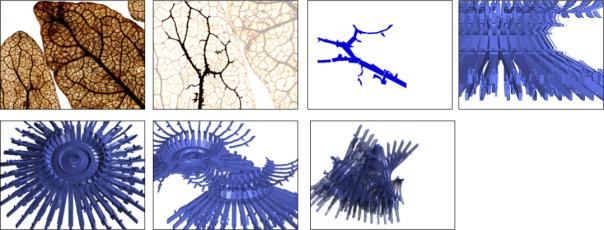
Abb.10
„Blattfiguren“[6]
Forms from nature impress us
frequently by their constructional sophistication and their visual complexity.
The wealth of form of nature is a constant source of inspiration for designers.
And, moreover, they usually can be clearly identified as "forms of
nature", i.e. they definitively possess
"identity". In the following experiments we refer in each case
to an object (or a part of it) from nature. They are collected in the fall or
wintertime, when vegetation rests, as dried forms. They are usually small finds
[see Abb. 5], and they are prepared between the two glasses of a photographic
slide. The “slide” is then scanned in a digital scanner The material received
this way is the raw material for the digital (student) experiments which we
want to discuss the following section.
From the collected and digitally
prepared natural forms, three-dimensional objects are generated, using any of
the CAD-systems commen in designing. The students work with different programs
and tehey were used in the experiments. For the production of the
three-dimensional objects only selected and prespecified transformations are allowed.
They can however be used repeatedly and in any order.
Strictly
only the following transformations are allowed:
- Extrude
contour (or plane)
- Scale, rotate, shift
- Duplicate,
add
- Cut
The
goal is, to generate three-dimensional, sculptural objects, which stimulate
“architectonic fantasies”
We
regard the results of each transformational chain now under the criterion of
the preservation or the destruction of "identity. The simple, however
difficult to answer question is: Is there something remaining in the produced
spatial object, which can be recognised in its identity and attributed to the
natural form it started from? Since the transformational chain may be bridging
many steps, we can also ask: After which step do we recognize, that the object
has clearly departed from the starting form? We begin with a simple example
[Abb.2].
The
programme has seven steps and the identity of the starting object is somehow
recognizable. The programme is as follows:
- Vectorize
the leave and fill plane
- Cut along
axis of symmetry and erase left part
- Extrude
- Scale
- Rotate and
copy
- Construct a
vertical swinging line from copied elements
- Rotate this
line around vertical axis and copy 40 times
A
different Situation is shown in the following figures [Abb. 7, Abb. 8, Abb. 9], which each show a
generative sequence. Especially the Fig. 9 is showing in towards the end of the
sequence a complete loss of the identity of the starting figure.
In the
following sequences [Abb. 10, Abb. 11, Abb. 12] some „architectural“ images are
emerging, but, despite their complexity, it seems to be possible to identify
their origin from the given starting point. A similar situation is encountered
in the last two examples [Abb. 13, Abb. 14] too.
The
following observations from the experiments may be notable:
1.
The
generated images have an own identity. In all cases this identity is somehow
unique.
2.
Only
in some cases a transport of identity from the start object to the final object
is observable
3.
The
images are of a nature, which would be difficult to achieve deliberately
4.
Surprisingly
few transformations are needed to arrive at the final object
5.
Only
very basic transformations – off the shelf of standard software – is needed
6.
There
is no specific and obvious use of the generated images. They are digital games
7.
The
results are however highly inspiring and a practical use can pop up any time
8.
It is difficult o formulate rules, in the sense of recommendations to
follow a preferable sequence of transformations
9.
The discussed “experiments” (student work), have a deficit with respect
to mechanisms of controlling the experiment
10.
In most cases it seems the students were “carried away” as they
proceeded
11.
It seems possible, with a little experience, to manipulate the results
into wanted directions
References
[1] First constructed by Ottmar Körzell, then by Ole Werner
[2] Martin
Güntert, http://www.uni-kassel.de/~dehlwww/Grundlagen2/
[3] Susanne Hermann,
http://www.uni-kassel.de/~dehlwww/Grundlagen2/
[4] Christian Poppel,
http://www.uni-kassel.de/~dehlwww/Grundlagen2/
[5] Anne Schmitz,
http://www.uni-kassel.de/~dehlwww/Grundlagen2/
[6] Jens Otten,
http://www.uni-kassel.de/~dehlwww/Grundlagen2/