 |
 |
 |
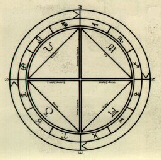
| Cerchio, triangolo, quadrato, forme primordiali dell'universo, secondo il giapponese Sengai | Il ciclo zodiacale, delle dottrine cosmologiche islamiche, secondo Ikhwàn Al-Safà | Calcolo della quadratura del cerchio in una tavoletta babilonese |
ADATTABILITÀ AL
CONTORNO
( COMPOSIZIONE E ARTICOLAZIONE
SPAZIALE VERSATILE)
 |
 |
 |
| Cerchio, triangolo, quadrato, forme primordiali dell'universo, secondo il giapponese Sengai | Il ciclo zodiacale, delle dottrine cosmologiche islamiche, secondo Ikhwàn Al-Safà | Calcolo della quadratura del cerchio in una tavoletta babilonese |
 |
 |
| Favo d'ape | Configurazione dei cristalli di neve |
Il triangolo, il quadrato e il cerchio furono figure fondamentali fin dall'antichità (cinese, indiana, greca, araba, romana), in quanto figure che affondano le loro radici in una comune mitologia primordiale, e da cui presero l'avvio la scienza dei numeri fondata sulle simbologie cosmologiche e gli ordinamenti politico-religiosi teocratici, quindi le antiche scienze tipo l'alchimia, e le concezioni di civiltà fondate sul numero tre e il numero quattro. "La stessa concezione del Mandala e della quadratura del circolo sul piano matematico, e della configurazione dell'universo sul piano cosmologico, e della fondazione della città sul piano urbanistico, e della cupola sul piano architettonico, e del disco cromatico sul piano della teoria del colore, si spiegano con questo comune denominatore". (A. Marcolli, "Teoria del Campo 2", Sansoni Editore, Firenze 1991)
Le figure geometriche di base, che nascono dalla lettura soggettiva che facciamo dall'immaginario di riferimento soggettivo, e che assumiamo come strumento per tessere lo spazio, sono due poligoni regolari, il quadrato e il triangolo equilatero coordinate nell'esagono regolare, ricordando che il fondamento di questa coordinazione è nella circolarità o sfericità del modello.
Qual è la struttura del quadrato?
 |
Disegniamo le sue diagonali e le sue mediane, due linee che collegano ciascuna due vertici opposti, e altre due linee che collegano ciascuna le metà dei due lati opposti. Queste quattro linee si incontrano in un punto centrale. Le due mediane sono tra loro perpendicolari (come le due diagonali) i punti o nodi caratteristici sono 5: i 4 vertici e il punto centrale.
 |
 |
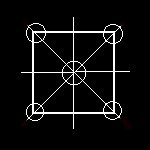 |
Ecco è questa la struttura del quadrato, perfettamente riconoscibile. Se infatti disegniamo a parte due rette perpendicolari, e altre due rette perpendicolari ruotate di 45° rispetto alle precedenti e che si incrociano tutte nel medesimo punto, vediamo che questa è la struttura non di un solo quadrato, ma di tutti i quadrati possibili, dal più piccolo al più grande, l'uno dentro l'altro.
 |
 |
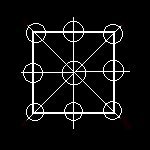 |
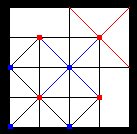
Nell'ultima immagine ci siamo soffermati nuovamente su un solo quadrato, e abbiamo considerato parte integrante della sua struttura anche i 4 lati che lo delineano. Vediamo ora che la struttura di uno specifico è formata da otto linee: i 4 lati, le due diagonali, le due mediane; e da nove nodi o intersezioni: i quattro vertici, i quattro punti mediani dei quattro lati, e il punto centrale.
"Possedere la struttura di un campo significa anche possedere tutta la sua articolazione formale"(A. Marcolli, "Teoria del campo", Sansoni Editore, Firenze 1991). Infatti continuando con l'esempio di un singolo quadrato osserviamo che i quattro punti delle mediane possono essere visti come i 4 vertici di un altro quadrato più piccolo del precedente, e ruotato di 45°; in cui le mediane sono le diagonali e le diagonali sono le mediane del quadrato più grande. Possiamo anche continuare: dal nuovo quadrato possiamo pervenire ad un altro più piccolo collegando i 4 punti mediani e invertendo le diagonali e le mediane, e così via, procedendo verso l'interno. Il movimento può anche essere invertito, costruendo tutta una serie di quadrati alternati dall'interno all'esterno, ogni volta facendo diventare punti mediani i vertici, e diagonali le mediane prolungate dal quadrato precedente. Questo sviluppo alternato generale può anche essere settorializzato, quando osserviamo che le due mediane dividono il quadrato in 4 parti che sono 4 quadrati. Scegliamone uno, per esempio quello in alto a sinistra, e su questo costruiamo una serie di quadrati alternati procedendo verso l'interno.
 |
 |
 |
Abbiamo visto qual è la struttura del quadrato in generale e di ogni quadrato in particolare. Questa struttura è il supporto portante della forma, la struttura che permette il massimo di articolazione formale. Ma esiste una seconda struttura modulare: essa è quella che denota e caratterizza un certo discorso all'interno del campo, che permette cioè di avere molteplici sviluppi compositivi. Già abbiamo detto che le due mediane dividono il quadrato in 4 quadrati interni più piccoli. Questi 4 quadrati sono sottomultipli del quadrato più grande che li comprende: il lato di ciascuno è la metà del lato del quadrato più grande. Vediamo quindi che la struttura modulare parte da una suddivisione in parti uguali dei lati del campo e da un tracciamento di rette parallele ai lati, che partono dai punti di suddivisione. Le parti uguali sono moduli che formano famiglie di quadrati più piccoli all'interno del quadrato più grande che li comprende. Il modulo è il sottomultiplo: metà, un quarto, un ottavo.., del quadrato di base.
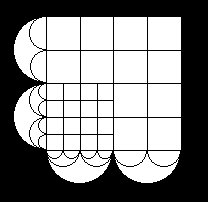 |
Qual è la struttura del triangolo equilatero?
 |
La sua struttura portante è costituita da sole tre linee che chiameremo mediane se le consideriamo dalla parte di ciascun lato, e che chiameremo diagonali se le consideriamo dalla parte di ciascun vertice. Scomponendo deduciamo che su queste tre linee strutturali passanti per un punto centrale poggiano tutti gli infiniti triangoli equilateri che possiamo immaginare.
 |
 |
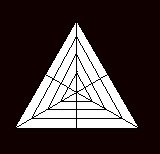 |
Prendiamo quindi in considerazione un solo triangolo equilatero. Possiamo inscrivervi un altro triangolo equilatero i cui punti di vertice poggiano sui tre punti mediani del triangolo precedente; mentre le mediane diagonali continuano ad essere le stesse. Si può costruire così con sviluppo alternato, tutta una serie di triangoli equilateri, l'uno capovolto rispetto all'altro, con movimento verso l'interno, e sempre più piccoli, o con movimento verso l'esterno, e sempre più grandi.
Ma questo sviluppo alternato può anche avvenire in un settore parziale del triangolo di base. Costruito il primo triangolo interno, con vertici appoggiati ai punti mediani del triangolo dato, osserviamo come questo primo triangolo divide il campo in 4 triangoli equilateri uguali, tre dei quali sono dislocati ai vertici ed uno, rovesciato, al centro, che è poi lo stesso triangolo che ha suddiviso modularmente il campo. In uno di questi 4 triangoli procediamo con il medesimo sviluppo alternato, che ora sarà parziale rispetto al campo.
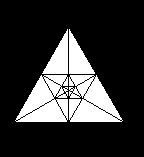 |
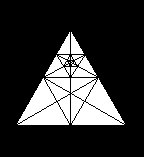 |
Individuiamo anche la struttura modulare suddividendo i lati in segmenti di uguale misura, sottomultipli dei lati del campo. Da ogni punto della suddivisione, sui tre lati, conduciamo le rette parallele a tutti i lati del triangolo di base, parallele cioè al perimetro del campo.
 |
Una volta addotte le figure di base che utilizzeremo per "tricoter" lo spazio è necessario procedurizzare il loro impiego, ossia definirne il loro possibile utilizzo o il criterio di scelta di una configurazione anziché di un'altra a seconda non solo del contorno ma anche di altri parametri per noi importanti. Sappiamo che sul piano, con poligoni regolari singolarmente presi, possiamo ottenere triangolazioni, esagonazioni, quadratazioni. Critchlow (nel libro "The order in space") fa le seguenti considerazioni a proposito di questi modelli: 1) il pattern triangolare realizza il massimo di strutturazione statica, 2) il pattern esagonale ( di cui non abbiamo definito la struttura in precedenza perché lo riteniamo una forma generata sempre partendo da un triangolo equilatero ruotato su un suo vertice) realizza il massimo di configurazione spaziale, 3) il pattern triangolare è intermedio. Queste sono leggi che noi adduciamo da Critchlow, ossia regole che ci permetteranno di scegliere un pattern non solo in base alla configurazione geometrica del contorno ma anche in base alle considerazioni sopra dette. Le tre forme regolari danno luogo ad una seconda serie di tessiture modulari, le strutture modulari coprenti. Vediamo così che partendo da una maglia triangolare avremo una maglia coprente esagonale, con la maglia esagonale avremo un maglia coprente triangolare, e con la maglia quadrangolare avremo una maglia coprente quadrangolare.
 |
 |
 |
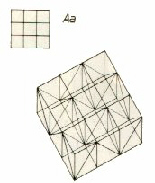
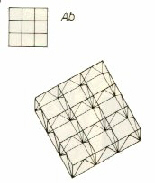
Dagli schemi grafici elaborati da due architetti francesi contemporanei, J. P. Colmant e A. Laplace, adduciamo le caratteristiche di alcune combinazioni spaziali fra due configurazioni spaziali piane:
 |
 |
 |
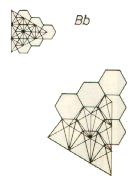 |
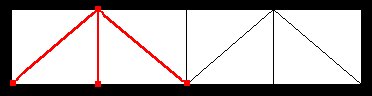
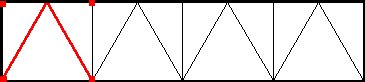
Essenzialmente si può parlare di due tipi di strutture, la prima è formata da configurazioni modulari orizzontali identiche, con i nodi delle due griglie parallele situati sulla medesima verticale, all'interno di queste strutture si possono distinguere due casi, il primo in cui le aste oblique congiungono un nodo della modulazione superiore con un nodo di quella inferiore, il secondo in cui le aste oblique congiungono due nodi inferiori con il punto di mediana dell'asta superiore. Il secondo tipo di strutture sono formate da configurazioni modulari in cui i nodi di una configurazione piana sono situati sulle verticali dei centri delle maglie dell'altra configurazione. Anche qui si possono distinguere due casi, il primo in cui abbiamo due griglie orizzontali identiche, il secondo in cui abbiamo due griglie diverse, ma coordinate per forma (triangolo rispetto all'esagono,et...)
 |
 |
 |
 |
 |
 |