La sezione aurea è un rapporto geometrico che mi ha sempre affascinato per mettere in una relazione armonica due dimensioni. La formula che è alla sua base è che dividendo un segmento in due parti, una più lunga dellí 'altra, esiste un rapporto tale per cui la più lunga delle due sta al totale esattamente come la parte più corta sta alla più lunga.
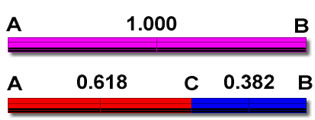
La distanza da A a B è
pari ad un' unità, per trovare la distanza AC è sufficiente
calcolare l' equazione 1:X=X:(1-X) che ci darà come risultato X=0.61803.
Esistono altri metodi per il calcolo della sezione aurea, come le serie
di Fibonacci, ma questo è uno dei più semplici ed intuitivi.
A proposito
della combinazione di numeri appena trovata, è molto interessante
notare subito come se al posto di 1 avessimo scelto come valore di partenza
1,618 (1+0,618), avremmo ottenuto il rapporto 1,618:1=1:0,618.
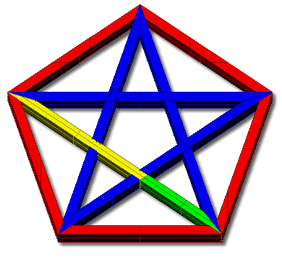
Ma esiste una figura geometrica
che racchiude al suo interno le proporzioni della sezione aure, il pentagono.
I suoi lati sono in rapporto aureo con le rette congiungenti due angoli
non continui (rappresentate in blu nel disegno a destro), ma non solo,
nel punto in cui due di queste rette si incontrano vengono divise in due
parti che sono ancora in rapporto aureo tra loro. Da questa osservazione
prendo il valore interno degli angoli che è di 36° e 72°.