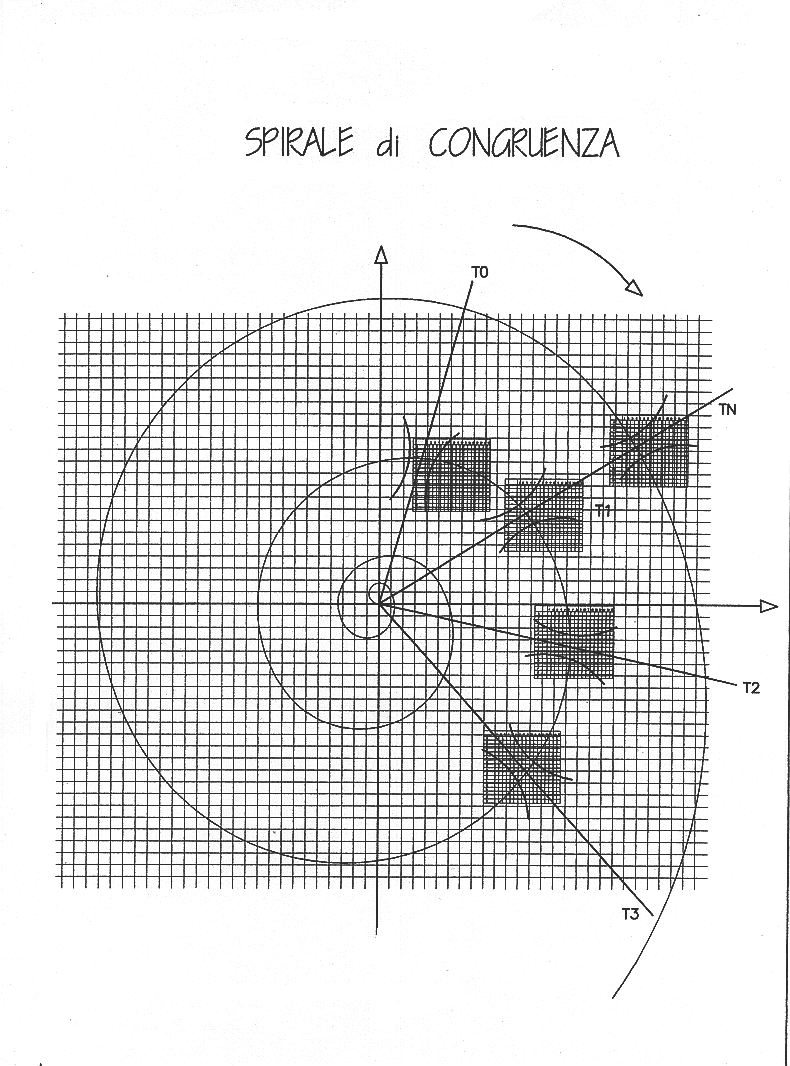
SPIRALE di CONGRUENZA
Al fine di studiare il legame esistente tra classe edificio e
temporalità tecnologica, tipo di facciata da 1 a 17, in altro luogo
spiegate, ed attribuire quindi al volume dell'edificio l'opportuna pelle
e soprattutto capire a che livello di temporalità un determinato
evento architettonico potesse concretizzarsi, si è osservato come
il sistema classe+pelle rispondesse ad un criterio, a parer nostro, lineare
di sviluppo.
Ad ogni temporalità di analisi del sistema si individua
uno spazio di dominio scandito da due iperboli, aventi la medesima retta
come asindoto.
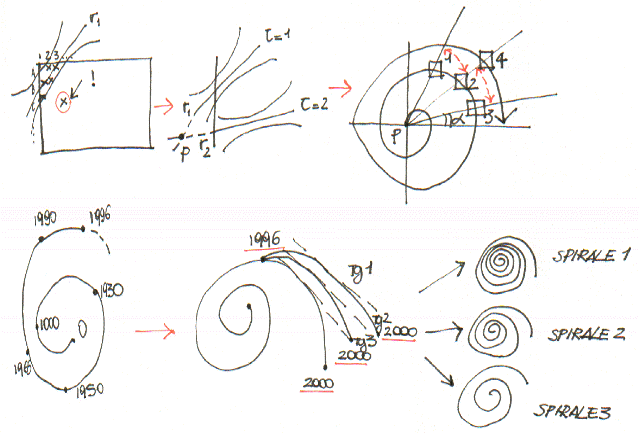 Cio' che sia compreso nell'intorno frastante le due iperboli, il
dominio, rappresenta pertanto la caratteristica inerente quella temporalità
stessa, gli elementi che rimangono esterni invece propongono le eccezioni.
Cio' che sia compreso nell'intorno frastante le due iperboli, il
dominio, rappresenta pertanto la caratteristica inerente quella temporalità
stessa, gli elementi che rimangono esterni invece propongono le eccezioni.
Il dato interessante, che ci preme di fare osservare, è
la crescita del sistema, l'aumento di complessità, il quale slitta
progressivamente nella direzione di classi più evolute, H - J -
L ...., e pelli più evolute, 14 - 15 - 16 - 17, al variare del tempo
ossia durante la rotazione che subisce la retta asindoto.
Notiamo quindi che per sistemi più sviluppati la retta
tende ad abbassarsi, a muoversi angolarmente, questo comporta la delineazione
di un dominio più evoluto.
Il centro P in cui convergono le rette delle temporalità
prese in considerazione viene ad essere il centro di una spirale evolutiva
del sistema.
Percio' gli scenari stessi vanno a coincidere con il tempo di
un punto della spirale, non precisamente delineato, giacchè non
ci interessa conoscere precisamente l'anno del sistema. Laddove incontriamo
rette di uguale coefficiente angolare, ma diverse temporalità, siamo
nella situazione di slittamento parallelo sulla spirale del sistema, possedente
quindi temporalità notevolmente più evoluta; l'intervallo
tra un sistema e l'altro può non essere costante. Le nostre specie
urbane sono una simulazione del sistema città a temporalità
non precisamente conosciute, ma sicuramente subenti un incremento evolutivo.
Per poter invece analizzare un sistema di sviluppo controllato,
con progressione angolare costante, è necessario sapere l'equazione
della spirale, ma questo aspetto appare indeterminato, perchè l'integrazione
ciclica delle tangenti successive può assumere diversi valori durante
la dinamica di sviluppo.