LA FASE GRAFICA MANUALE: IL METODO

Immaginiamo di lavorare su un’immagine bidimensionale che alluda - più o meno direttamente - ad una rappresentazione prospettica.

Se vogliamo riprodurne un modello tridimensionale, la prospettiva non ci è di alcun ausilio, in quanto non siamo in grado di misurare le dimensioni dell’oggetto o degli oggetti in essa rappresentati. Il metodo che intendiamo illustrare permette di ricavare un’assonometria - quindi una rappresentazione misurabile - dell’immagine prospettica in nostro possesso.

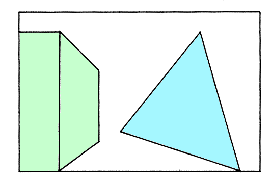
Consideriamo un semplice esempio di applicazione del metodo. Supponiamo di dover interpretare la seguente immagine:

Fig. 1.1

L’oggetto a destra lo interpretiamo come un pannello triangolare, posto in diversi modi nello spazio, quello a sinistra come due piani in prospettiva. Ecco un primo possibile codice di lettura.

Fig. 2.1

Ipotizziamo che l’elemento di sinistra sia una facciata di un volume in prospettiva, con un lato che ci sta di fronte e un altro di scorcio che poggia orizzontalmente sul terreno, il cui filo superiore è anch’esso orizzontale.

Le linee AB e CD dell’edificio convergono in un punto di fuga F. Facciamo passare per F una linea parallela alla base del quadro, fissando così l’altezza di osservazione (h). La nostra posizione sul piano assonometrico è assolutamente libera, basta semplicemente che ci mettiamo nel semipiano frontale al quadro. In questo caso ci collochiamo ortogonalmente al piano del quadro, ad una certa distanza da esso.

Vediamo come riportare in assonometria il pannello triangolare IEH.

Fig. 3.1

Il punto E coincide sia in prospettiva che in assonometria. Nella nostra lettura supponiamo che il punto H sia a terra, e che G sia la posizione a terra del punto I.

Con gli occhi (J) guardiamo il punto G e tracciamo il raggio visuale. Disegniamo la traccia del punto G sul pavimento, e conduciamo la retta passante per i nostri piedi (K) e per la suddetta traccia (G’). L’intersezione delle due rette appena disegnate determina la posizione, sul piano assonometrico, del punto G.

Per trovare I in assonometria (ricordando che G ne è la proiezione a terra sul quadro prospettico), conduciamo la verticale dal punto assonometrico corrispondente a G e tracciamo il raggio visuale passante per I. Il punto risultante è I in assonometria.

Per trovare H in assonometria, se ne disegna la traccia sul pavimento (H’) e si incrocia il raggio visuale passante per H con la retta passante per K e H’. Si determina così il pannello IEH in assonometria.

Disegniamo ora l’oggetto di sinistra in assonometria. Il lato frontale permane sia in prospettiva che in assonometria. Essendoci posti di fronte al punto di fuga F, il piano ABCD sarà perpendicolare al piano del disegno e parallelo ai lati longitudinali del piano assonometrico. Disegniamo la traccia di D sul pavimento (D’) e incrociamo il raggio visuale passante per D con la retta passante per K e D’; il punto risultante è il corrispettivo assonometrico di D.

Infine, tracciamo la verticale per l’ultimo punto assonometrico trovato e la incrociamo col raggio visuale per B. Ecco così determinato un possibile modello tridimensionale del quadro dato.

Se costruissimo un plastico delle dimensioni date dalla misura degli oggetti assonometrici, e guardassimo dal punto J ad altezza h, osserveremmo la stessa scena del quadro analizzato.

Un’altra lettura dell’immagine potrebbe essere la seguente:

Fig. 4.1

Il volume a sinistra viene interpretato come nel caso precedente; la nostra altezza d’osservazione è ancora h, però stavolta ci troviamo un po’ più a sinistra. Il punto I, inoltre, in prospettiva, cade a terra nel nuovo punto G. Ciò significa che il pannello triangolare è inclinato verso di noi.

Cominciamo dal volume di sinistra.

Fig. 5.1

Il lato frontale è sempre uguale, sia in assonometria che in prospettiva. Incrociamo il raggio visuale per D con la retta passante per K e D’: si trova D in assonometria. Si traccia la verticale per questo punto e la si incrocia col raggio visuale per B.

Passiamo al pannello triangolare: il segmento HE si trova a terra, E coincide sia in assonometria che in prospettiva, H si trova incrociando il raggio visuale per H con la retta passante per K e H’. Anche il punto I risulta agevole da ricavare, contrariamente a quanto si potrebbe pensare in un primo momento. Incrociamo il raggio visuale passante per G con la retta passante per K e G’. Da questo punto conduciamo la verticale e la incrociamo col raggio visuale per I.

Riportiamo, infine, una terza soluzione interpretativa.

Fig. 6.1

Siamo più bassi che nei casi precedenti, ed i nostri occhi sono alla stessa altezza del punto F, possibile linea di fuga della base dell’oggetto triangolare. Supponiamo che la proiezione del vertice I tocchi terra in G; che il lato HE poggi sul pavimento; e che pure il lato CD dell’edificio di sinistra sia a terra. Se prolunghiamo i lati AB e CD, individuiamo un punto di fuga che sta sopra l’orizzonte (F’). Ciò significa che il tetto dell’edificio è inclinato.

Ricaviamo l’assonometria del triangolo HIE (Fig. 7.1).

Fig. 7.1

Il corrispettivo assonometrico di H si trova incrociando la retta per K e H’ col raggio visuale per H. Il corrispettivo di G si trova incrociando la retta per K e G’ col raggio visuale per G; per questo punto si traccia una verticale, che incrociandosi con il raggio visuale per I, fornisce il corrispettivo assonometrico di I. Congiungendo i due punti appena trovati con il punto E si ottiene la vista assonometrica del pannello HIE.

Per quanto riguarda il volume di sinistra, il corrispettivo di D lo si trova incrociando la retta per K e D’ col raggio visuale per D. Dal punto appena trovato si conduce la verticale e la si incrocia col raggio visuale passante per B. Misurando con un righello la lunghezza del lato assonometrico AC, si può constatare che gli spigoli AC e BD non sono uguali.

Il metodo appena esaminato può essere impiegato in una vasta casistica di immagini bidimensionali, da quelle che alludono direttamente alle tre dimensioni - come i dipinti realizzati secondo i codici canonici della prospettiva -, a quelle che sono difficilmente interpretabili tridimensionalmente in assenza di codici di lettura capaci di attivare meccanismi di creazione della forma (morfogenesi) - come i quadri di arte moderna -.

In teoria non vi è alcuna limitazione alle supposizioni che si possono fare sul tipo di organizzazione spaziale celata nell’immagine bidimensionale su cui si sta operando.

Nello specifico delle due tavole oggetto della nostra sperimentazione, prima ancora dell’attivazione del metodo appena esaminato, siamo stati indotti ad alcune considerazioni.

Innanzitutto ambedue le tavole permettono l’individuazione di due punti di fuga - uno a sinistra e uno a destra del disegno -, che sono luogo di convergenza delle linee che delimitano la gran parte dei volumi architettonici raffigurati. Queste linee si percepiscono come appartenenti a piani orizzontali, quindi la retta che unisce detti punti di fuga può essere interpretata come linea dell’orizzonte. Tale supposizione si può considerare fondata qualora la linea dell’orizzonte così individuata si riveli parallela alla base della tavola. In tal modo quest’ultima può essere assunta come linea di terra.

La distanza tra la linea di terra e la linea dell’orizzonte rappresenta l’altezza dell’osservatore. L’elemento ancora incognito è la posizione dell’osservatore. Questa non può essere individuata a partire dal disegno prospettico, senza effettuare delle ipotesi aggiuntive. Per capire quali possano essere queste ipotesi, è necessaria una breve digressione.

Quando si esegue una prospettiva accidentale, il procedimento di individuazione dei punti di fuga si configura, in pianta, come segue:

Fig. 8.1

Si disegna la pianta dell’oggetto da ritrarre in prospettiva - o il rettangolo che la contiene - inclinata dell’angolo a che si ritiene più opportuno; si posiziona il punto di vista V dell’osservatore in un punto a piacere, ad una certa distanza dal quadro, e si conducono da questo punto le parallele ai lati dell’oggetto. I punti d’incontro di dette parallele con il quadro individuano i due punti di fuga cercati.

Dal momento che nel nostro caso i punti di fuga sono noti, è la posizione dell’osservatore da determinarsi.

Se facciamo il precedente ragionamento a ritroso, però, ci rendiamo conto che posizionando la traccia dell’osservatore in un punto qualsiasi del semipiano frontale del quadro, è assai probabile le l’assonometria prodotta rappresenti dei volumi che in pianta non sono costituiti da spigoli ortogonali.

Fig. 9.1

Osservando le tavole di Piranesi e Sant’Elia, invece, si ha proprio la sensazione opposta, confermata dal fatto che questa è la circostanza più ricorrente in architettura. Per tale motivo abbiamo intuito che la traccia dell’osservatore andrebbe posizionata in un punto appartenente alla semicirconferenza il cui diametro coincide con la congiungente i due fuochi (Fig. 10.1). In tal modo le rette che in prospettiva concorrono in quei due fuochi, in pianta sono sempre ortogonali, secondo un corollario della geometria elementare che specifica che ogni angolo inscritto in una semicirconferenza è retto.

Fig. 10.1

Questa è stata una nostra precisa scelta, che il metodo non specifica, in quanto si occupa semplicemente di ricavare un’assonometria da una prospettiva.

Inoltre, per comodità, abbiamo deciso di porre l’osservatore in posizione decentrata rispetto al quadro, principalmente per facilitare la costruzione.

Il tipo di assonometria che si è voluto ottenere, sia nel caso di Piranesi che in quello di Sant’Elia, è stata l’assonometria monometrica, posizionando l’osservatore in modo tale che gli angoli del triangolo inscritto nella semicirconferenza fossero pari a 30 e 60 gradi .

Fig. 11.1

Nel lavoro di esecuzione del disegno assonometrico abbiamo evitato di seguire pedissequamente i segni dell’artista sulla tavola, considerandoli talvolta delle semplici indicazioni di massima su ciò che lui intendeva andasse fatto.

Ci siamo così trovati a collaborare con lui, interpretando o addirittura inventando, laddove pareva necessario, eseguendo così un progetto.

L’impegno maggiore ha riguardato la ricerca continua della plausibilità e della verosimiglianza. Accanto a tali esigenze ci siamo posti il traguardo di realizzare dei modelli che rispondessero alle nostre personali convinzioni estetiche.

Per questo motivo - soprattutto nel caso della tavola di Piranesi, che riporta alcune linee della prima versione -, abbiamo tralasciato di indagare quelle che conducevano a contraddizioni evidenti di senso, che avrebbero portato a degli esiti formalmente più completi, ma in definitiva più confusi, e che avrebbero appesantito eccessivamente i modelli informatici.

Lo sforzo interpretativo della complessità sottesa dalle immagini bidimensionali ha portato, comunque, all’individuazione di bivi di senso che hanno fatto intravedere uno spettro di dinamiche evolutive del modello "in progress".

Il nostro modello è il risultato di una sola di queste dinamiche: è solo un evento fra tutti quelli possibili.