Intorno al 1200 tornò a Pisa e nel 1202 pubblicò il Liber abbaci, che contiene un'esposizione delle operazioni elementari con le cifre arabe, un'ampia trattazione delle frazioni, uno studio dei radicali quadratici e cubici e varie questioni di carattere algebrico e geometrico; particolare interesse rivestono alcuni capitoli che trattano di aritmetica commerciale. L'opera costituì per secoli un testo fondamentale di studio e contribuì efficacemente alla diffusione nel mondo occidenatale della notazione posizionale indoaraba.
Tra gli altri suoi scritti vanno ricordati la Practica geometriae (1220), un'opera a carattere didattico di geometria e trigonometria, e il Liber quadratorum (1225), che costituisce un brillante lavoro sulle equazioni indeterminate.
1:2=0.500 | 2:3=0.667 | 3:5=0.600 | 5:8=0.625 |
8:13=0.615 | 13:21=0.615 | 21:34=0.618 | 34:55=0.618 |
Più importante dal nostro punto di vista è però il fatto che il rapporto tra i due termini successivi si avvicina molto rapidamente a 0.618.
Sappiamo infatti che 0.618 è il rapporto della sezione aurea.
Per altra via si giunge a analoghe conclusioni.
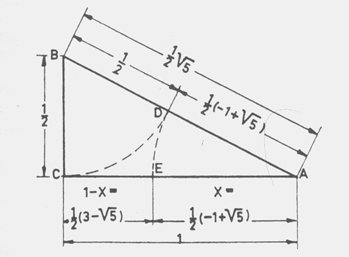
Se infatti dividiamo un segmento di lunghezza unitaria in una
parte maggiore X e in una minore 1-X tale che
(1-X):X=X:1
poiché nelle proporzioni il prodotto dei termini estremi è uguale
al prodotto dei termini medi:
X²=1-X
cioè
X²+X-1=0
da cui possiamo ricavare il valore di X:
X=½(-1±V(5))
poiché X deve essere positivo:
V(5)=2.236 -1+V(5)=1.236 ½(-1+V(5))=0.618
Possiamo allungare questo rapporto ad una proiezione
continua
(1-X):X=X:1=1:1/X, eccetera
0.382:0.618=0.618:1=1:1.618, eccetera