Nel 1958, il matematico Mandelbrot fu assunto presso il centro ricerche Thomas J. Watson di IBM.
Il suo primo risultato fu l'interruzione di un progetto di ricerca da milioni di dollari che si proponeva di eliminare il rumore che disturbava la trasmissioni dei segnali.
Quando esaminò tale rumore, Mandelbrot scoprì una struttura intricata ma familiare che gli suggerì che la tecnologia in corso di sviluppo non sarebbe riuscita a tenere sotto controllo il problema. Si rese conto che era semplicemente impossibile controllarlo o prevederlo. Si trattava infatti del caos.
Come ha potuto Mandelbrot comprendere la struttura intima del rumore di linea cosi rapidamente?

Mandelbrot chiamò questa somiglianza statistica di una parte all'intero invarianza di scala.
Le registrazioni di altri fenomeni imprevedibili, come le piene dei fiumi o l'andamento del mercato azionario, presentano la stessa struttura intimamente ciclica. Ciclica forse non è il termine più appropriato, anche se le curve preferite di Mandelbrot presentano cicli con cicli all'interno di altri cicli, ma nessuno dei cicli si ripete in modo del tutto esatto, anche se l’entità delle variazioni nelle curve rimane costante, le variazioni all’interno di altre variazioni le rendono imprevedibili in ogni punto di tempo e a qualsiasi livello di scala.
Mandelbrot aveva rilevato tale comportamento e iniziava a comprenderlo anche da un punto di vista matematico, ma non riusciva a convincere nessun altro della validità di questa teoria.
Le sue equazioni erano troppo astratte e le sue conclusioni troppo scomode.

Quanti potevano desiderare a quell’epoca una teoria che sosteneva che le cose erano complesse, incontrollabili e caotiche?
Questo non significava in sostanza che non esisteva nemmeno una teoria? Per oltre un decennio le bizzarre idee di Mandelbrot rimasero solo una sua personale ossessione.
Nel 1968, Mandelbrot strinse un sodalizio con un idrologo per studiare gli schemi ricorrenti nelle fluttuazioni del livello del Nilo, come i sette anni di opulenza e i sette anni di sciagure della Bibbia.
Insieme rilevarono le fluttuazioni e produssero poi dei falsi usando le formule di Mandelbrot. Quando questi grafici furono mostrati ad altri eminenti idrologi, nessuno fu in grado di distinguerli come falsi, anche se i grafici che erano stati preparati basandosi su modelli tradizionali venivano immediatamente riconosciuti come falsi.
Il realismo dei grafici dei Mandelbrot dimostrò in modo indiscutibile che si stava avvicinando con i suoi studi a qualcosa di importante. Egli continuò a produrre falsi di altri fenomeni caotici: prezzi del mercato azionario e dei beni, linee costiere e montagne. In tutti gli esperimenti le caratteristiche visive delle sue immagini erano affascinanti.
Come egli stesso ebbe modo di dire: "Prima, la gente voleva sfuggire ai miei scritti, ma nessuno poté sfuggire alle mie immagini".
Qual era il fattore segreto nei grafici di Mandelbrot che li rendeva assolutamente realistici?
Quale principio si annida dietro ai loro motivi visivi?
Si tratta semplicemente della dimensione frazionale di Hausdorff. Mandelbrot aveva intenzionalmente esplorato gli interspazi tra le dimensioni in cui erano accidentalmente incappati Cantor e Fournier cinquant’anni prima. Egli trasformò quelle strane rappresentazioni dell’infinito in ritratti realistici di fenomeni complessi naturali e sociali.
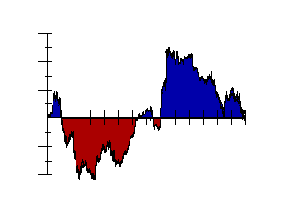
La figura mostra come Mandelbrot ha creato i suoi falsi. Tutti i fenomeni da lui studiati fluttuano tra alti e bassi ciclici, come la forma d’onda sinusoidale approssimata in questa figura. Ciò che rende così complesse le fluttuazioni è il fatto che contengono dei cicli all’interno di cicli più ampi. Per simulare tale andamento, Mandelbrot utilizzò tecniche di iterazione come quelle di Sierpinski e Koch.
La figura è una curva che si riflette in se stessa in questo modo. Per creare la curva sulla destra, ogni piccolo rettangolo sulla sinistra diventa un gruppo di rettangoli più piccoli con la medesima disposizione. Ognuno di questi rettangoli più piccoli diventa a sua volta un gruppo a forma sinusoidale di rettangoli ancora più sottili, fino a quando ogni rettangolo e troppo piccolo per essere riconoscibile.
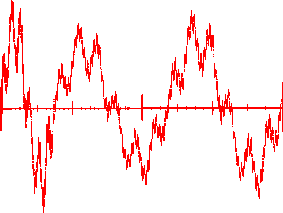
Mandelbrot completò i suoi falsi introducendo un fattore casuale ad ogni fase, in modo che la curva non risultasse periodica e artificialmente regolare
La figura raggiunge un effetto analogo senza l’uso del fattore casuale. Differenziando ogni piccolo rettangolo in modo esclusivo, tramite estensione, rotazione o distorsione si raggiunge un grado di complessità pressoché indiscernibile dalla vera variazione casuale.