PLURIDIREZIONALITÀ

Questa immagine rappresenta un processo di raggiungimento di un possibile sviluppo nella tridimensionalità basato sulla applicazione della progressione numerica di Fibonacci, in questo caso sotto forma di Spirale, su piani diversi.

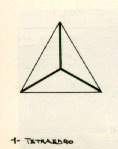
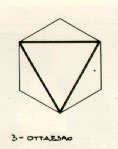
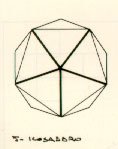
Come conseguenza diretta della tessitura dei campi con poligoni regolari (triangolo equilatero e quadrato) e quindi della combinazione spaziale tra due configurazioni modulari piane, otteniamo delle cellule spaziali formate da solidi regolari che a loro volta si ottengono per la maggior parte, con moduli triangolari, "Si potrebbe dire che il processo di tridimensionalizzazione è una caratteristica prevalente del triangolo" A. Marcolli, "Teoria del campo 2", Sansoni Editore, Firenze 1991; infatti con il triangolo formiamo il tetraedro (4 triangoli equilateri), l'ottaedro (8 triangoli equilateri), l'icosaedro (20 triangoli equilateri). Con la modulazione piana quadrata formiamo invece un solo solido, il cubo o icosaedro.

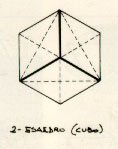L'aggregazione di più solidi regolari uguali forma una struttura spaziale. Immaginando di esplodere i solidi come possiamo unire i lati negli spigoli, oppure unire un solido ad un'altro? Dobbiamo lavorare negli spigoli considerandoli nodi da cui dipartono le aste in varie direzioni e con angoli diversi. Ma quale può essere la migliore configurazione formale del nodo?

Aggiungiamo al nostro immaginario di riferimento soggettivo queste immagini del sistema MERO come riferimento tecnico da cui addurre alcune regole che saranno utili al nostro progetto. Diamo qui di seguito una breve descrizione tecnica degli elementi che compongono questo sistema: il sistema " MERO " , ideato dal noto ingegnere tedesco Mengeringhausen, è apparso sul mercato nel 1943 col nome MEngeringhausen ROhrkonstruktion. A quell'epoca fu il primo sistema spaziale del mondo la cui fabbricazione fosse stabilita su base industriale mediante la produzione in serie degli elementi componenti. L'elemento fondamentale del sistema è il nodo, costituito da una sfera in acciaio, sfaccettata a poliedro, che presenta 18 fori filettati e quindi può riunire fino a 18 aste. Le aste normalmente realizzate con tubi a sezione circolare o quadrata, risultano tutte di ugual lunghezza, rastremate all'estremità e fissate alle sfere di nodo per mezzo di bulloni ad alta resistenza. Le estremità dei tubi sono munite di una vite prigioniera sulla quale si avvita un manicotto che funge da dado: ruotando il manicotto si fa uscire inizialmente la vite filettata per una lunghezza pari alla penetrazione nel relativo foro del nodo; facendo quindi girare il manicotto insieme con la vite, si fissa questa nel foro; il bloccaggio finale si ottiene serrando il manicotto contro l'estremità del tubo.

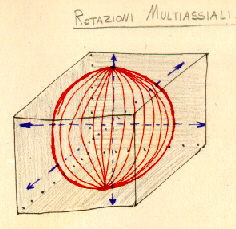
Ma dopo questo breve preambolo che ci consente comunque di comprendere il sistema tecnologico adottato nel nodo mero, passiamo alla nostra lettura soggettiva di questa immagine tecnica di riferimento: poco sopra ci siamo chiesti quale fosse la migliore configurazione formale del nodo, ora affermiamo che la sfera risponde alle nostre esigenze, perchè permette di ottenere angolazioni idonee per la composizione di poligoni regolari, e perche può alloggiare numerose aste senza problemi di natura statica. Ora cercheremo di capire la struttura della sfera da quali regole è formata, cercheremo di addurre quelle regole che ci interessa importare nel nostro progetto.

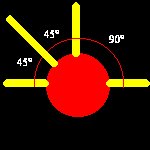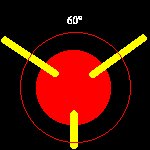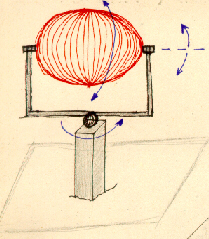
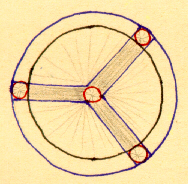
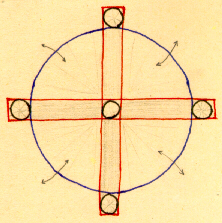
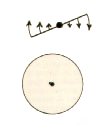
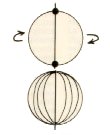
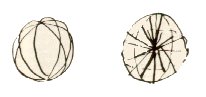
Possiamo vedere la sfera come costituita da tutta una serie di cerchi dello stesso diametro, diversamente orientati nello spazio ma legati ad uno stesso diametro in due punti polari, o addirittura generata da un solo cerchio che ruota attorno ad un diametro e questa è la struttura modulare della sfera. Ma possiamo anche vedere la sfera come proiezione in tutte le direzioni dello spazio di tanti raggi uguali uscenti da un solo punto, il centro della sfera, e questa è la struttura portante

Ora che abbiamo addotto le modalità relative alla genesi della forma sfera andremo a cercare all'interno di un altro sistema di giunzione di segmenti convergenti in uno stesso punto dello spazio. A questo proposito ci sembra molto interessante un sistema proposto dalla società Kee Klamp la quale ha sviluppato una serie di giunti adatti alla realizzazione di strutture tubolari di tutti i tipi; ciò che più ci interessa, e quindi ciò che vogliamo addurre e importare come regola nel nostro progetto, è la sempilicità del sistema e soprattutto la possibilità di poter ottenere una uguale capacità di connessione di segmenti (tubolari) convergenti in un punto dello spazio con diverse angolazioni. Oltretutto riteniamo interessante il fatto che questi giunti siano morfologicamente differenziati l'uno dall'altro in base al numero di tubolari da connettere, alle angolazioni possibili, agli agganci con altri elementi.

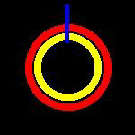Il sistema è basato su un connessione cilindrica di dimensione superiore al tubolare che deve alloggiare, i due elementi sono bloccati da un terzo elemento a brugola che permette di ottenere una chiusura sicura tra tubo e giunto.