Le linee guida       Catalizzatori            Paradigma organizzativo  Progetti d'ispirazione   Codici  

 Scenari             Progetto                  Osservazioni             Link utili 

Le regole:

LA LUMINOSITA'

regola 1, la luminosità: Il rapporto tra superficie finestrata e calpestabile all'interno della stanza deve essere maggiore o uguale a 1/6 e maggiore di 1/3 della superficie opaca. L'edificio così risulta luminoso negli interni quando c'è luce naturale, e risalta luminosamente quando fuori è buio.

regola 2, la modellazione della superficie di base:  Le aperture non devono giacere sullo stesso piano, ma il susseguirsi di superfici opache e trasparenti deve svolgersi su piani spezzati. Gli spigoli devono essere ben definiti, i bordi chiari e leggibili. L'edificio risulta così spigoloso, riflette e rifrange la luce, dando l'idea della luminosità.

regola 3, la logica radiale: Per rendere più luminosi gli elementi si sceglieranno logiche radiali di operazioni

LA NATURALEZZA

regola 4, la sovrapposizione delle superfici: Le parti spigolose saranno coperte e svelate da elementi morbidi e fluenti. Questo rende l'edificio molto naturale in quanto nella natura tutto è sovrapposizione di dolce e aspro. Inoltre lo stesso celare e rivelare delle linee sinuose dona all'edificio sensualità.

regola 5, la relazione tra le superfici : Le superfici morbide e quelle spigolose stanno in rapporto quantitativo1:2.

regola 6, la modellazione della superficie di sovrapposizione: La curvatura delle superfici deve essere tale per cui l'altezza della curva è 2/6 della sua lunghezza.

regola 7, l'asimmetria:  Nella natura tutto è la negazione e il contrario di tutto, ogni cosa ha in sé le due facce della medaglia: la linea e la curva, l'angolo e il complementare di esso, la norma e l'eccezione, la simmetria e l'imperfezione di essa. Questo è vero nel microscopico, come nel macroscopico. Per esempio il paesaggio di Lecco è imperfettamente asimmetrico, infatti, alle montagne spigolose corrispondono le morbide linee del lago.

Per  rendere il concetto di asimmetria bisogna eseguire la progettazione solo su metà dello spazio e costruire seguendo le regole della elaborazione asimmetrica.

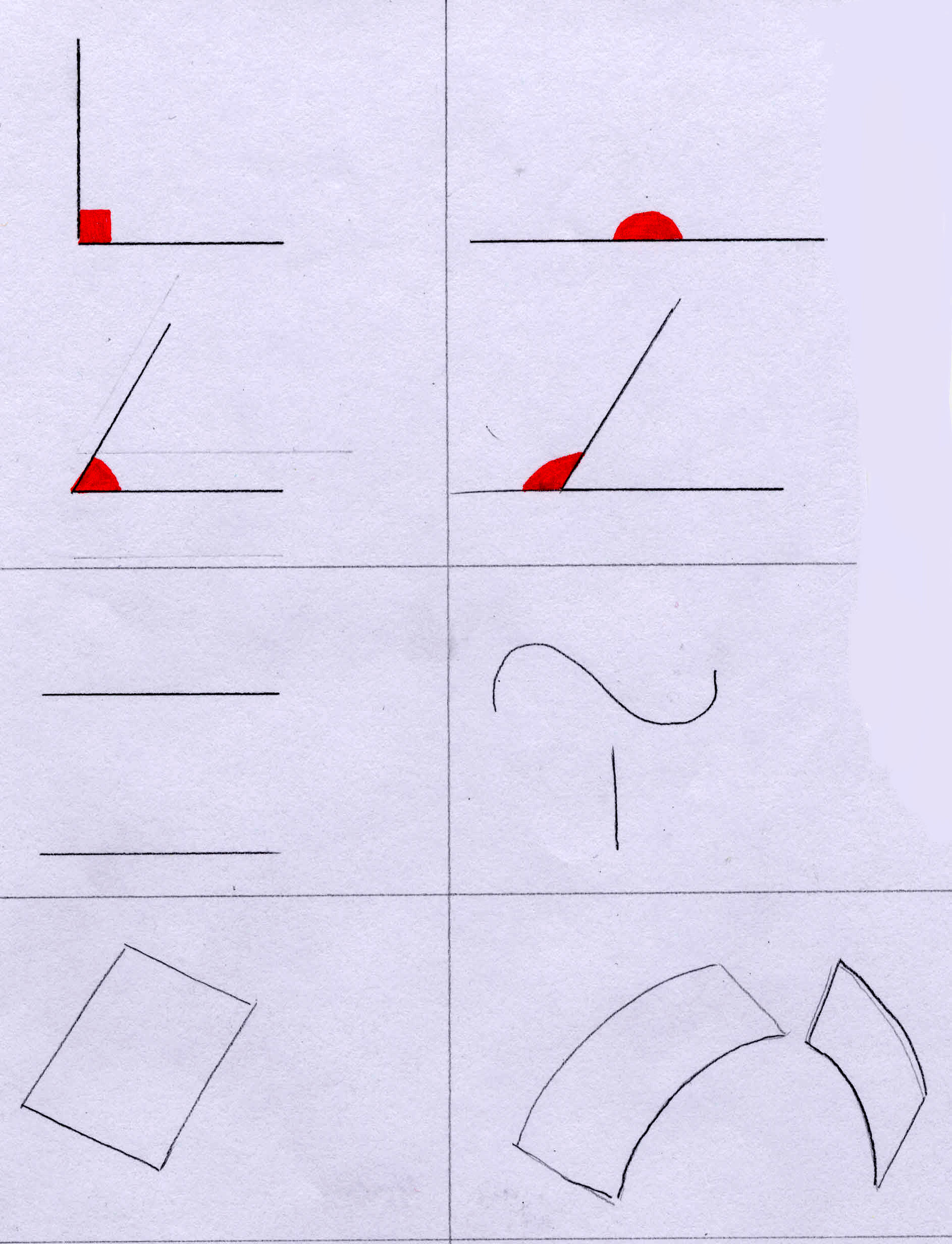
-Si individua un asse o una superficie secondo la quale costruire l'asimmetria. Nell'edificio è il piano passante tra le due superfici: quella curva e quella spigolosa.

-Ogni linea spezzata diviene una curva.

-A superfici piane corrispondono superfici concave o convesse.

-A spazi chiusi seguono spazi aperti.

-Al cubo si accosta la sfera; al parallelepipedo l'ellisse; al cerchio il quadrato o un poligono.

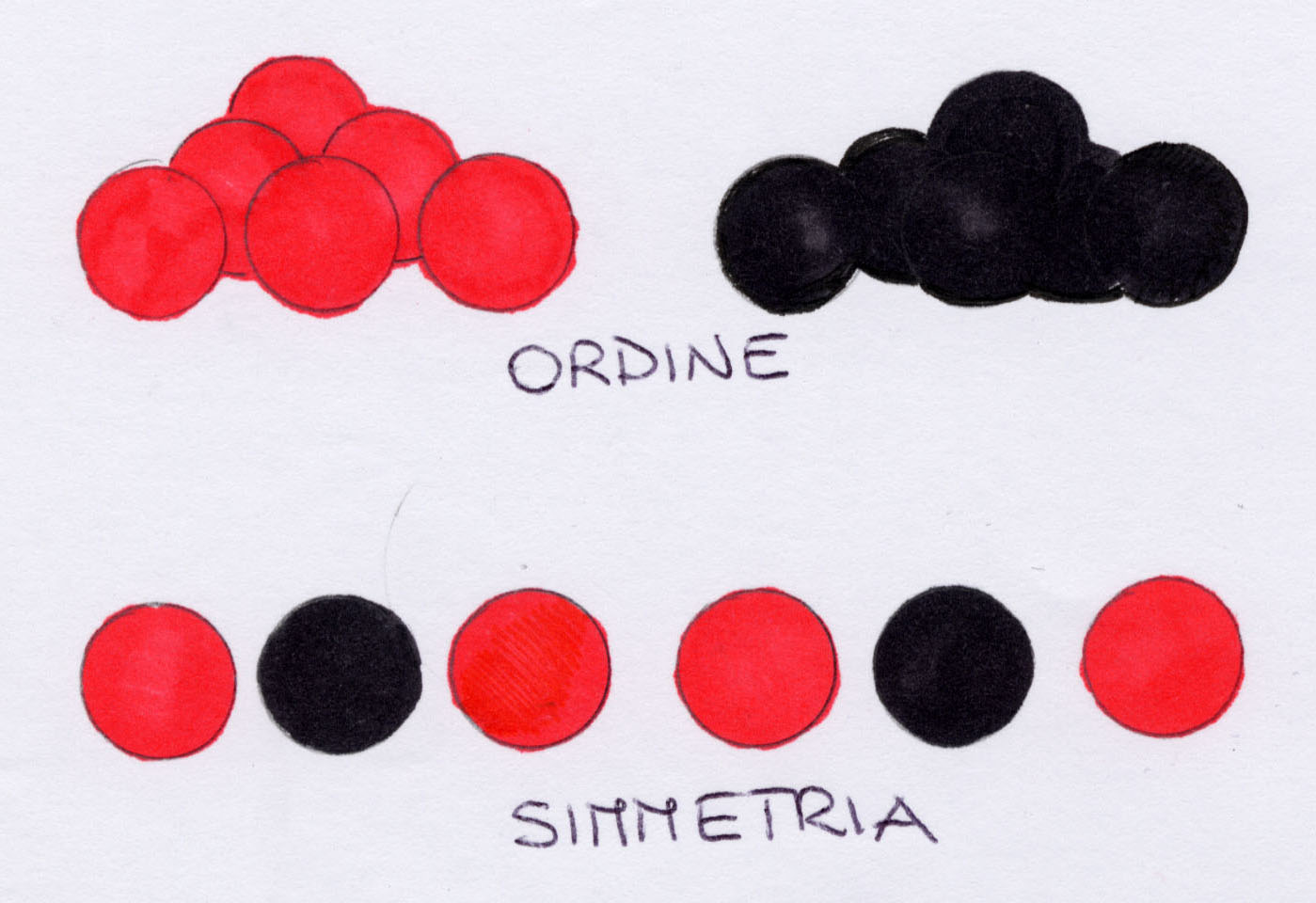
regola 8, l'ordine : E' molto affascinante notare che nella natura l'ordine è antipodico rispetto alla simmetria. Si osservi per esempio che se ci sono delle palline rosse e delle palline nere, se si vorrà fare ordine si metteranno le nere da una parte e le rosse dall'altra. La simmetria invece prevedrebbe l'alternarsi di palline rosse e di quelle nere. Questa è una dei fondamenti della fisica dello stato solido, ovvero della fisica a livello atomico.

LA NATURALEZZA SI FA FASCINO

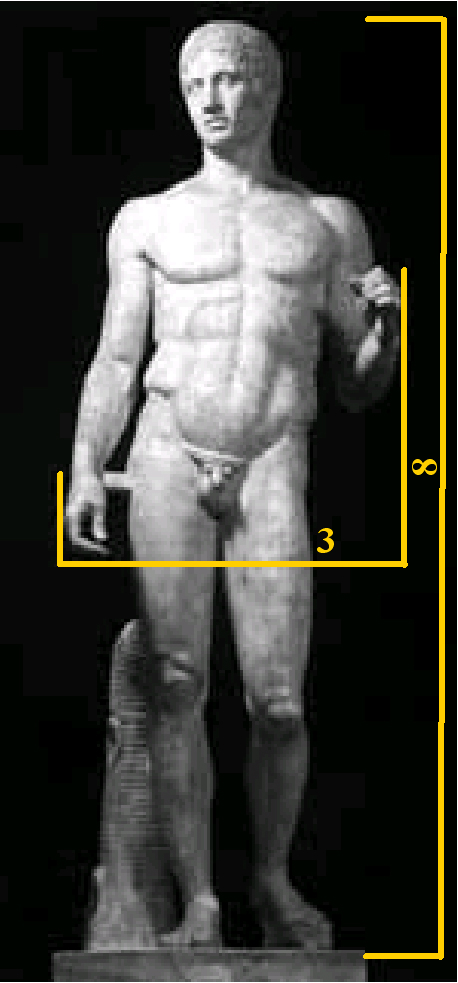
Nella natura è fondamentale la regola della proporzione. Nulla infatti sembra sguaiato o eccessivo. Immediato è in tal senso il richiamo all'antichità. Il fascino dei corpi delle statue trae forza dal richiamo alla natura e della trasformazione della stessa in pura  proporzione, armonia ed equilibrio. Nell'antichità greca la natura diviene così fascino, inteso come fascino intellettuale. Si traggono le seguenti regole:

regola 9, la proporzione : L'oggetto deve risultare proporzionato anche se possono esistere delle differenze anche importanti nella dimensione delle sue parti. La parte maggiore dell'elemento non dovrà essere inferiore ai 2/5 della dimensione dello spazio in cui è inserito.

Secondo il canone greco policleteo inoltre la dimensione minore è pari o superiore ai 3/8 di quella maggiore.

La parte intera può essere divisa in modo armonioso con la riduzione in moduli:la dimensione maggiore è divisibile in tre unità. Così per esempio un angolo, o un segmento possono essere diviso armoniosamente in tre parti uguali .

regola 10, l'armonia: La sezione aurea è quella parte di un segmento che è la media proporzionale fra il segmento intero e la parte restante di esso. Su questa equazione l'architettura classica e rinascimentale fondava il principio compositivo della sua armonia proporzionale. In tutti i canoni classici dell'architettura la sezione aurea costituisce lo strumento principe con cui vengono scanditi e proporzionati le basi, le colonne, i capitelli e le trabeazioni. Nell'architettura rinascimentale veniva comunemente usato il rapporto aureo sia per suddividere e partizionare armonicamente le facciate dell'edificio,sia per proporzionare volumetricamente gli ambienti.

Metodo analitico per la divisione di un segmento in rapporto aureo.

Sia dato un segmento AB, si prenda sul segmento AB un punto P che divide il segmento AB in due parti disuguali a e b. Si dice che il punto P è la sezione aurea del segmento AB se il rapporto tra l'intero segmento AB ed il segmento maggiore a è uguale al rapporto tra il segmento maggiore a ed il segmento minore b,  se è soddisfatta cioè la seguente relazione:

risolvendo la proporzione si ottiene la seguente equazione di secondo grado:

 a² - ab - b²  = 0

Per trovare la sezione aurea di un segmento basta moltiplicare la lunghezza del segmento dato per 0,618 e si ottiene la lunghezza del segmento maggiore a.
Se invece si conosce la lunghezza del segmento a e si vuol trovare la lunghezza del segmento AB che ha per sezione aurea il segmento a basta moltiplicare la lunghezza del segmento a per 1,618 per ottenere la lunghezza di AB.

Metodo grafico per la divisione di un segmento in rapporto aureo.

regola 11, la giunzione tra le curve :Le curve,quando di curvatura differente vengono unite tra loro attraverso un fillet di 20°

IL FASCINO

regola 12, la sinuosità: 

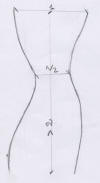La sinuosità è data dagli elementi curvi che ripropongono le essenziali  proporzioni femminili: la parte centrale dell'elemento misura la metà rispetto a quella soprastante e a quella sottostante. L'altezza dell'elemento deve essere maggiore al doppio dalla parte più larga. La parte inferiore si conclude con un restringimento che può variare dal 20% al 100%.

oppure

regola 13, lo svelare:

Il nascondersi e il mostrarsi delle linee aspre avviene grazie alla sovrapposizione di un elemento curvo, adagiato come un velo sulla facciata. Il velo avvolge la facciata. Esso partirà da un angolo per chiudersi in un altro angolo. Avrà un rigonfiamento nella parte centrale.

        Scenari