Ho creato dall'inizio una semplice tabella dove poter elencare le varie attività sportive praticabili sia in un ambiente coperto che in uno all'aperto. A questo punto ho dovuto pormi il primo limite ovvero dare due dimensioni massime e minime di attività sportive svolte rispettivamente all'aperto e al coperto : la pista di Atletica ed il campo da Basket .
Così ho escluso, ad esempio, il campo da baseball in quanto non solo complica una eventuale predisposizione alla polifunzionalità, ma è una attività sportiva poco praticata nel nostro Paese e con una conseguente scarsa partecipazione di spettatori. Per quanto riguarda il campo da pugilato ( il ring ), è facilmente ricavabile da una pedana sopraelevata posta sul campo da basket con la possibilità di ricavare i posti a sedere su di un unico piano come verrà illustrato più avanti nello "schema di visibilità". Infine, la dimensione spaziale, l'ingombro della struttura dipende ovviamente non solo dalla dimensione massima del campo da gioco ma anche dal numero di spettatori disposti sulle varie gradinate. I nuovi regolamenti prevedono il conteggio dei posti solo a sedere eliminando i posti in piedi in quanto "scomodi" per motivi di sicurezza . Inoltre si richiede al progettista di tenere al coperto la quasi totalità dei posti a sedere. Al fine della progettazione, ho scelto indicativamente un numero massimo di posti a sedere all'interno della mia struttura polifunzionale nella conformazione adatta ad ospitare competizioni di atletica leggera : circa 80.000 spettatori .
Figura 35 - Matrici fruibilità
E' l'argomento principale del lavoro
svolto, lo scheletro, la parte portante di tutto il progetto.
Per la progettazione delle tribune mi sono
avvalso della equazione parabolica per determinare l'inclinazione
delle gradinate. Come possiamo notare dallo schema
esemplificativo qui sotto riportato nell'equazione parabolica
Y = [ F/ LD ] X 2 + [ ( H / D ) + ( F / L ) ] X + H

Figura 36 - Schema dell'equazione parabolica
Y è l'altezza cercata per l'occhio di ciascun spettatore rispetto al piano orizzontale contenente il punto assunto come oggetto della visione ed è in funzione di :
H = è il valore dell'ordinata Y assunta per il primo spettatore, cioè l'altezza del suo occhio rispetto al medesimo piano orizzontale ;
D = è la proiezione in orizzontale della distanza tra il primo occhio e il punto O oggetto della visione ;
L = è la distanza tra due successive file di posti, supposta costante ;
F = è l'altezza della fronte dello spettatore pari a cm 12 ;
X = è l'ascissa, avente come origine il punto, nel quale è situato il primo spettatore : di essa interessano i valori discreti D, D + L, .... , D + nL, relativi alla posizione dei singoli punti di vista.
Figura 37 - Esempio 1
Il primo esempio che può essere paragonato al caso delle balconate di un teatro, esiste un rapporto tra la distanza del pubblico dal centro di attrazione e l'altezza ove il pubblico stesso risiede. Questo sistema può essere utile nel caso si dovessero realizzare delle suites negli stadi, come tuttora è in voga nei mega-stadi americani.
Gli esempi seguenti dimostrano che minore è l'angolo di inclinazione delle gradinate maggiore è la distanza che deve avere lo spettatore dal campo da gioco.
Altri casi dimostrano che alzando il livello sul piano orizzontale del centro di attrazione possono diminuire l'inclinazione delle gradinate. Tale livello non può superare di molto la linea di visibilità della prima riga dello spettatore per evitare che questi non possa assistere alle azioni svolte all'interno del campo da gioco.
Figura 38 - Esempio 2
Figura 39 - Esempio 3
Infine, per riuscire ad ottenere una bassa inclinazione delle gradinate si è potuto agire sulla disposizione dei posti a sedere : una sistemazione a scacchiera dei seggiolini, fa in modo che nonostante la compresenza sulla stessa linea di due spettatori non infastidisca la visibilità dell'uno sull'altro. Tale sistemazione può essere utilizzata nel caso si prevedesse una polifunzionalità dello stadio, e precisamente, nell'utilizzo di una struttura a cassettiera come verrà spiegato successivamente nel capitolo riguardante le tecnologie per la creazione di strutture polifunzionali.
Figura 40 - Disposizione a scacchiera
Nella seguente illustrazione viene disegnata la linea parabolica continua, oltre il limite di visibilità.
L'altezza e l'alzata dei gradoni è la variabile per rispettare la precedente equazione , quindi, all'aumentare della distanza dello spettatore dal centro campo, aumenta l'alzata. A questo punto, per rimanere nei limiti della normativa tedesca, spezzo la curva della parabola, ricavando tre settori.
Figura 41 - Parabola
Questi tre settori, traslati orizzontalmente creano tre livelli differenti ( che costituiscono la base per la creazione dei tre anelli ).
Le alzate di ogni anello sono state uniformate per comodità in modo tale da ottenere delle misure standard con precisi rapporti :
| Posizione anello | Alzata | Pedata | Rapporto |
| primo | 24 cm | 72 cm | 1 : 3 |
| secondo | 40 cm 40 cm |
80 cm 72 cm |
1 : 2 1 : 2 |
| terzo | 60 cm 70 cm |
70 cm 80 cm |
1 : 1 1 : 1 |
Un caso particolare è dovuto al sistema di tribune a "cassettiera" per soluzioni polifunzionali in cui la disposizione dei posti è a scacchiera quindi risulta l'alzata di 25 cm e la pedata di 160 cm.
Per sviluppare la matrice costruttiva della gradinata ho dovuto seguire un procedimento a ritroso, ovvero, partire dal particolare per giungere al generale, costruendo i singoli distinti casi e poi un sistema che potesse riassumere tutti i casi precedentemente analizzati.
Dopo aver effettuato tale operazione, mi sono accorto che i punti di visibilità dei tre anelli non convergono tutti in uno unico. Così ho dovuto applicare delle trasformazioni come illustrato successivamente :
- spostamento del piano da gioco rispetto il punto di incontro delle due rette di visibilità superiori ;
- spostamento orizzontale del primo anello.
Per costruire tutto ciò ho dovuto pormi alcuni limiti :
Inoltre, come ho già detto precedentemente, ho utilizzato rapporti standard tra alzata e pedata.
Esiste non solo la suddetta normativa tedesca ma anche una seconda normativa detta "inglese" che differisce dalla precedente per la lunghezza del raggio ( 190 m ) misurato dall'angolo del campo da gioco. Tale normativa è più severa della prima consentendo quindi un minore sviluppo delle tribune.
Figura 42 - Limiti di visibilità
Si ottiene l'arco limite di visibilità creando una semicirconferenza dal punto centrale del campo ad un metro dal livello del campo da gioco stesso. Inoltre per quanto riguarda la visibilità dell'ultimo spettatore delle successive tribune, non deve avere alcun ostacolo dinanzi a sé nell'arco di 15 m sulla perpendicolare al centro campo.
Ho applicato un limite per quanto riguarda il numero di anelli o ring delle tribune, ponendo tale numero massimo uguale a tre.
Figura 43 - Costruzione del limite di visibilità
Nella seguente tabella (
tabel-01) ho sviluppato uno schema evolutivo delle tribune
ponendo come variabili sull'asse delle ascisse la lunghezza dal
centro del campo da gioco ; sulle ordinate, l'altezza minima
e massima delle singole tribune. Inoltre si è venuta a creare
una nuova variabile che è rappresentata dall'angolo di
inclinazione delle tribune che viene posta arbitrariamente uguale
all'angolo di inclinazione di visibilità dell'ultimo spettatore
posto sul secondo anello, con un intervallo di 5 °(gradi ).
Figura 44 - Schema evolutivo delle tribune.
Figura 45 - Esempi di evoluzioni delle tribune
Ho quindi creato alcuni esempi di evoluzioni delle tribune dove la lunghezza di ogni singolo anello è determinato dai vari intervalli dell'angolo di inclinazione della linea di visibilità dell'ultimo spettatore. Un'altra possibilità compositivo-tematica della struttura "tribuna" è costituita dal dominio di un anello sull'altro, ovvero la precedenza di una tribuna sull'altra facendo in modo che la visibilità dell'ultimo spettatore non venga limitata dalle tribune sovrastanti.
Figura 46 - Dominio delle tribune

Figura 47 - Tribuna singola ( Pista di Atletica -
lato maggiore )
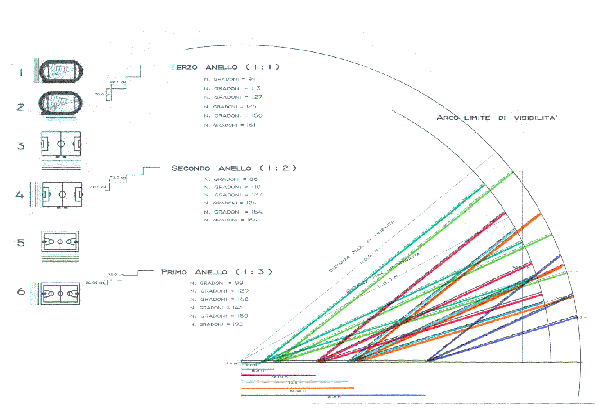
Figura 48 - Tribuna singola - Comparazione dei limiti di visibilità

Figura 49 - Tribuna a tre anelli ( Pista di
Atletica - lato maggiore )

Figura 50 - Tribuna a tre anelli ( Pista di Atletica - lato minore )

Figura 51 - Tribuna a tre
anelli ( Campo da Basket - lato maggiore )

Figura 52 - Tribuna a tre anelli ( Campo da Basket - lato minore )

Figura 53 - Tribuna composta ( Pista di Atletica -
lato maggiore )

Figura 54 - Tribuna composta ( divisione in uguale numero di gradoni )
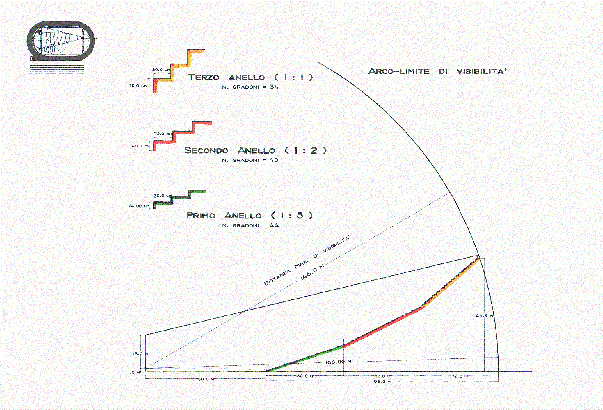
Figura 55 - Tribuna composta ( divisione in parti uguali )

Figura 56 - Tribuna a tre anelli ( punti diversi di visibilità
sul campo )
La seconda parte fondamentale per creare lo "scheletro" della forma-stadio, è la matrice generativa dei percorsi. Tale matrice si ottiene dal perimetro dei campi da gioco e precisamente da quella forma che può contenere tutte le altre forme delle attività sportive da me prese in considerazione. Così le forme geometriche maggiormente utilizzate derivano dall'ovale della pista di atletica e dal rettangolo del campo da basket. Tali percorsi possono essere costituiti da linee spezzate o linee chiuse, o ancora , curve e lineari ; così pure le linee di raccordo possono essere curve o lineari. Il cerchio è quella figura geometrica che ovviamente può contenere qualsiasi forma ma purtroppo crea anche una grossa fascia di spazio inutilizzabile, aumentando l'ingombro di tutta la struttura. Ad eccezione dei quadrilateri, altre figure geometriche inscritte al cerchio, come ad esempio pentagoni, esagoni ecc., sono poco funzionali per lo stesso motivo sopra citato.
I percorsi devono successivamente rispondere alla richiesta di polifunzionalità della struttura Per questo motivo, come verrà spiegato più avanti, alcuni percorsi risultano inutilizzabili ed altri utilizzabili solo con determinate modifiche.
I percorsi si sviluppano su di un unico piano ; l'eccezione che conduce ad una tipologia inconsueta è la spirale. Tale eccezione comporta un aumento di complessità totale, "è capace di operare dei ribaltamenti di paradigma che consentono la proliferazione degli scenari virtuali".
3.4 - Matrice Sezioni - Pilastri
Figura 57 - Sezione dello Stadio delle Alpi -Torino
Individuati i percorsi generativi, le varie inclinazioni e disposizioni delle tribune, per completare definitivamente l'oggetto che genera lo stadio, devo studiarne la sezione, la struttura portante, quindi le pilastrature . Le sezioni possono essere realizzate in svariati modi : negli esempi seguenti ho tentato di creare un paradigma organizzativo di tali elementi partendo da soluzioni semplici fino a raggiungere una maggior complessità formale. Tale paradigma organizzativo è stato sviluppato attorno ad un unico anello per esemplificare un procedimento che andrà poi a modificarsi a seconda delle richieste fatte al sistema. Anche per quanto riguarda questo capitolo, è stato importante avere come riferimento degli immaginari di sezioni di stadi già esistenti verificando le varie inclinazioni delle tribune, gli spazi da esse create e quindi il rapporto tra vuoto e pieno. L'evento eccezionale che interviene nelle evoluzioni delle sezioni è l'arco. L'arco contamina dapprima l'elemento "gradoni", poi la struttura portante.

Figura 58 - Immaginario di riferimento delle sezioni.
La divisione in settori delle tribune, è generata nella maggior parte dei casi dalla linea dei percorsi generativi. Nel caso tali percorsi siano a "linea chiusa", il ritmo delle divisioni in settori è scandito dalla posizione delle scale e dalle vie di uscita. Ho successivamente sviluppato una serie di possibilità formali delle vie di uscita delle tribune ; partendo dal rettangolo, la forma più comunemente usata, sono giunto a soluzioni più complesse, usando processi adduttivi, facendo interagire figure geometriche semplici. Successivamente ho studiato il rapporto tra scale e vie di uscita, sia sotto un puro aspetto formale, che sotto l'aspetto vincolo-progettuale . Tale aspetto, ovviamente, è quello dominante ; in base alle normative progettuali si può determinare l'ampiezza dei settori, quindi il numero di spettatori per ogni settore, in relazione anche alla dimensione delle vie di uscita. I vincoli progettuali, utilizzati per questa sezione, sono rappresentati nella figura sottostante e rispettano gli standard della Gazzetta Ufficiale, n.85 dell'11 aprile 1996.
" La capienza di ciascun settore non può essere superiore a 10.000 spettatori per impianti all'aperto e a 4.000 per quelli al chiuso ".
" La larghezza di ogni uscita e via d'uscita deve essere non inferiore a 2 moduli ( 1.20 m ) ; la larghezza complessiva delle uscite deve essere dimensionata per una capacità di deflusso non superiore a 250 ( 1.20 m ogni 500 persone ) per gli impianti all'aperto ed 50 ( 1.20 m ogni 100 persone ) per gli impianti al chiuso...".
" I percorsi di smistamento non possono avere larghezza inferiore a 1.20 m e servire più di 20 posti per fila e per parte ; ogni 15 file di gradoni deve essere realizzato un passaggio, parallelo alle file stesse, di larghezza non inferiore a 1.20 m ; è consentito non prevedere tali passaggi quando i percorsi di smistamento adducono direttamente alle vie di uscita ".
Figura 59 - Istituto Central de Restauracion (particolare della cupola ) - Madrid
I primi stadi avevano, in genere, solo la "tribuna d'onore" coperta. Oggigiorno è buona norma avere tutti i posti a sedere, al coperto. Poi, con l'avvento dei super-stadi americani, si è arrivati alla copertura integrale degli stadi. Nell'evoluzione morfogenetica dello stadio l'elemento "copertura" gioca un ruolo molto importante nell'immagine formale. Il disequilibrio viene ora creato dal rapporto tra chiuso e aperto . Tale rapporto è capace di variare completamente la forma "stadio" avvicinandosi alla tipologia del "palazzetto dello sport". Seguendo la strada della polifunzionalità, e quindi della mobilità strutturale, si apre la sfida progettuale per raggiungere una specie chiamata con un nuovo nome, "poli-stadio", con una semi-copertura che può tramutarsi in una copertura totale. Un ruolo di notevole importanza viene svolto dai materiali costruttivi, tecnologici : muratura, cemento armato, acciaio, vetro, legno, tensostrutture in nylon ecc.
I metodi per passare da una struttura a chiusura parziale ad una totale devono essere di facile impiego utilizzando tecnologie alla portata dell'ingegneria attuale come semplici movimenti che consentano a grosse coperture ad arco di scorrere lungo binari o a tensostrutture amovibili di creare una forma dinamica e mutevole.
L'idea più innovativa è la realizzazione di una calotta che può essere costituita da una parte fissa ed una mobile a scomparsa. Questa idea, scaturita grazie alla metodologia utilizzata, necessita ovviamente di tecnologie più avanzate e quindi la sua realizzazione appartiene ad uno spazio temporale evolutivo futuro.
Al fine di raggiungere la polifunzionalità all'interno dello stadio ho utilizzato tre diverse soluzioni tecnologiche :
A) lo spostamento su binari del primo anello verso l'interno dello stadio
B) l'elevazione o l'abbassamento del campo da gioco
C) l'apertura delle gradinate del primo anello a modo di cassetto.
Queste soluzioni mirano a migliorare la
visibilità nel momento in cui vengono intraprese attività che
necessitano spazi di gioco minori rispetto alla massima
dimensione della pista di atletica.
Figura 60 - Esempi di polifunzionalità
Figura 61 - Esempio di funzionalità del sistema a "cassettiera"