A questo punto, dalle adduzioni fatte, ricaverò delle matrici che inserirò in una tabella, di modo tale che, ad ogni adduzione fatta corrisponderà o corrisponderanno delle matrici.
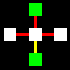
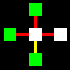
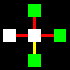
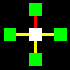
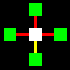
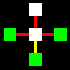
La matrice base sarà costituita da un quadrato centrale legato con un altro quadrato per ognuno dei suoi quattro lati, attraverso le relazioni orizzontali di collegamento e non-collegamento (gialla e rossa).
Naturalmente i cinque quadrati di ogni matrice potranno essere di colore diverso, a secondo che identifichino uno spazio interno-blu, uno spazio intermedio-bianco, o uno spazio esterno-verde.
Di conseguenza ci troveremo di fronte a diverse matrici, caratterizzate dalle diverse combinazioni tra i tre modelli di spazio (BLU-BIANCO-VERDE) e i due tipi di relazione (GIALLO-ROSSO).
Tutto ciò significa che ogni matrice rappresenta uno spazio, che sarà definito dal cono al suo interno, e come è posto nei confronti del suo intorno.
Per capire meglio il passaggio dall'adduzione alle matrici ottenute ho inserito un esempio animato riferito allo stoà di Samos.

Questo è un caso in cui le matrici ottenute da inserire nella tabella sono tutte e tre diverse nelle loro differenti combinazioni, ma può capitare che nella stessa adduzione esistano più matrici uguali, che nella tabella verranno naturalmente raccolte sotto una stessa combinazione.
Questo procedimento l'ho attuato per ogni adduzione, livello per livello, difatti nella tabella ho diversificato le matrici anche secondo il livello da terra da cui le ho ricavate.

DIPINTO DI ALTDORFER	PIANO TERRA
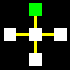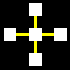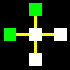	PIANO PRIMO
STOA' DI SAMOS	PIANO TERRA
DIPINTO DI RAFFAELLO	PIANO TERRA
TOGU NA DI KOKORO	PIANO TERRA
TOGU NA DI IRELI CANAL	PIANO TERRA
DIPINTO DI CIMA DA CONEGLIANO	PIANO TERRA
STOA' DI DELOS	PIANO TERRA
DIPINTO DI MARQUET	PIANO TERRA
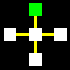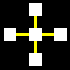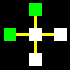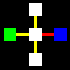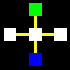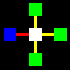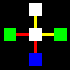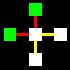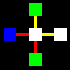STOA' DI MOLYKREION	PIANO TERRA